[2024-09-29 note: This was previously posted on Cohost, on 2022-11-19 at https://cohost.org/ireneista/post/365371-sokoban-and-on-and but the irenes.space URL is the permanent one.]
[originally posted to Twitter in August 2021; this is the first of a series of three threads we made about Sokoban, and probably the most interesting of the three]
We've been using our pandemic-related free time, in part, to catch up on things we always meant to do but never got around to. The latest thing for us is playing the original 50 Sokoban levels.
It has come to our attention that there are people who have not heard of Sokoban, possibly because they don't fantasize about being forced to solve difficult puzzles. That is fair! But we will explain what it is.
Sokoban was one of the earliest block-pushing games, dating to 1982. We recall, in the day, hearing that it had won a prestigious award; our memory says it was an award for boardgames and puzzles, since videogame awards weren't a thing in those days.
We can't find information about what award that would have been, though.
[since this writing, we got a System 7 emulator working and dug up MacSokoban, the first version of it we ever played. the README there says "The original Sokoban was the winner of a computer game contest held in Japan in the early 80's. If you know who the original programmer was, please enlighten me. The game became a commercial success on NEC computers." it also references a Curses version (a Unix terminal library) as where the author of MacSokoban learned about the game.]
It was, as far as we're aware, the first game to thoroughly explore the design space of puzzles you could make out of blocks on a square grid. All the same size blocks, pushing only, no holes or other mechanics. This was where it started.
You've almost certainly played Sokoban-style puzzles as side-quests in long story-driven games, and there's a whole genre of puzzlers that are essentially twists on the Sokoban mechanics.
Even in games as superficially different from Sokoban as Baba Is You, you can see the same basic pushing mechanics, and a lot of the same puzzle-solving concepts will help you.
In our opinion, the original Sokoban levels are pretty hard, compared to most puzzle games before and since. There's a good reason for that, which is most players don't want such a frustrating experience. :>
This thread, and our effort to reconnect with this particular piece of the past, was inspired by watching a streamer we like, a very smart person, play a puzzle game that involved block-pushing and realizing they don't have the basic ideas that help us get through Sokoban.
It's not their fault, to be clear. You have to learn this stuff by doing it, and easier games don't give you the kind of testbed you need to teach yourself the ground rules, because you can get away with missing things.
When we say ground rules, we mean things like:
Four blocks in a tight square can never be separated.
A block against the wall can never be moved off the wall, unless you can push it off the end of the wall.
Little lemmas, that you prove for yourself and then they become shorthands that let you avoid losing moves without having to think through the details every time.
Part of our goal in writing about this is to kind of put it forward as an opportunity for self-guided study, for anyone who wants to get better at this stuff. In our entirely subjective opinion, learning to break problems down like this is a useful life skill.
Of course, we would say that, since we put so many points into that metaphorical skill tree, in our life. So make your own decision whether it's worth it for you.
In addition to the process of kind of always looking for helpful little rules you can prove to simplify the problem, the other bit thing we take from these puzzles is learning to think of problems in terms of the state space.
We should define "state space", for people who don't have the math or CS background. Consider the very first Sokoban level:
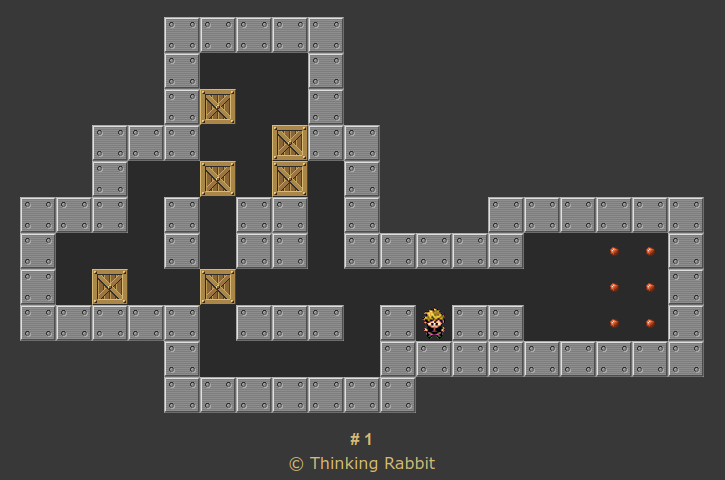
The state of the puzzle is the locations of the blocks, and where the player is standing. Six blocks, at those six specific spots, and the player at that spot in the bottom right.
If the player moves upward exactly one space, now the puzzle is in a different state:
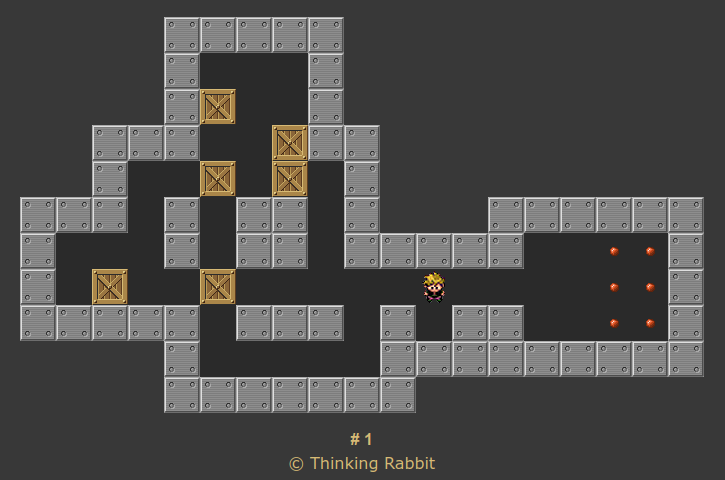
But it's not a very interesting difference, is it? After all, the player can always move back down, and then you'll be in the exact same state you started in.
If you're trying to solve the puzzle, it makes sense to group these two states together in your head. They're basically the same, because you know that you can always go back and forth between them. So you don't need to keep track of them separately.
In fact, since there's no one-way arrows or anything in Sokoban, the player can walk anywhere they want, and as long as they are just walking, not pushing things, it makes sense to think of all those states as the same.
But suppose the player has the temerity to push a block:
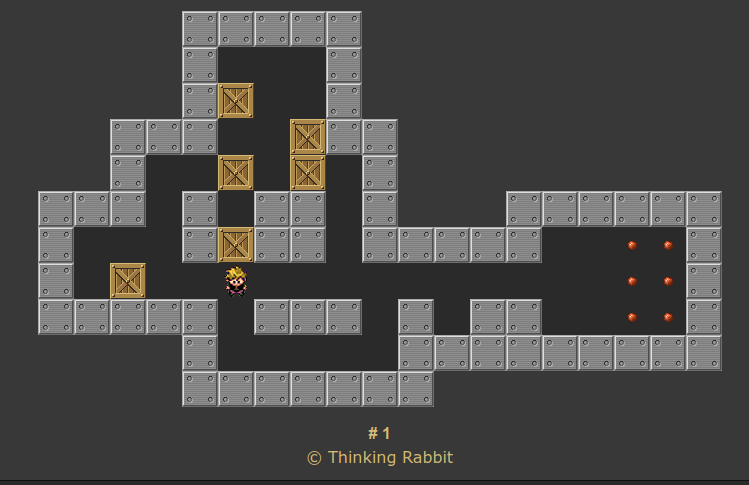
Ah! Now they have changed the world! It's not immediately obvious whether they can get back to the world where they didn't do that. This may very well be an irrevocable decision.
It's a meaningful change. Now there is a map connection through that T-junction. The player can walk through the junction and reach the stuff on the other side. The total area they can walk around in is bigger.
In some cases, there are ways to push blocks that don't really change anything. You push them but you could easily push them back. It's very useful to pay attention to which ones those are.
This is not one of those easily reversible decisions. The block is in the hallway, and there's no way to get behind it and push it out, unless you push something else first.
So when we say that we're thinking in terms of the state-space, one of the big pieces of what we mean by that is that we're always paying attention to which things are reversible, and we're not doing irreversible things without a good reason.
The other piece is where the "space" comes from. We build a map in our head, of all the different states the puzzle could be in, and how they connect.
Like in terms of where this move fits in the overall map, we know that it opens things up a bit - it lets us access that leftmost crate if we want to. It does lead to a lot of nearby states where there's a crate blocking the hallway above the T-junction, and that's a downside.
We don't have the solution to puzzle 1 in our head, but just from thinking in terms of the state space, we're already pretty sure that pushing that crate was a losing move (we did it for the sake of an example).
We could be wrong, there could turn out to be something we haven't foreseen, but from a quick glance, what it looks like is that there isn't going to be any way to push the crate at the other end of the vertical hall to the side.
We have to push that top crate, the one directly above the one we pushed, sideways at some point in the solution. That's if there is a solution that can be reached from here. We have to because there's no other way to get behind the one we pushed and get it out again.
We can't push the top crate to the right, unless we've already cleared up the mess with the two crates over that way, because it would form an immovable 2x2 square with the nearby crate and the walls below them.
We can't push it to the left because we can't get to the right side of it, unless we already clear up that same mess.
We can't push it down, even if we could clear up the mess keeping us from reaching it, because pushing it down would form an immovable 2x2 square in the hallway below it (actually two of them, depending on how you count).
So you see how we use those little lemmas, the tiny rules we proved for ourselves, to help us figure out what parts of the state space are worth exploring.
Just from this same sort of reasoning, we're almost certain the actual first move in the solution, if we started over, would be to go up that right-side hallway and push the crate at the end of it left.
That's a guess, but we're confident of it. We made that guess because we know that it doesn't do anything that's obviously difficult to reverse, in the way that pushing a crate into a hallway does.
It could still get us into trouble, we can't prove that it's reversible, but in terms of how much trouble it creates, it's less than the move we showed.
Okay. So this is what we get out of Sokoban. Thought we'd share, hope you liked reading about it. :)
If you want to play, it turns out there's a convenient browser version, though we suspect it may not work well on mobile: https://sokoban.info
Our recommendation would be to try to get past the first 50 levels, but don't worry about completing the thousands of other levels this site has. The first 50 were the original; the "original & extra" pack on the site has those plus the decades-old expansion pack of 40 more.
You'll probably learn whatever you're going to learn within those first 50, it gets quite difficult.
As kids, we got to the late 40s but we never finished, so our aim with this replay is to get through level 50. We're up to 34 so far, and we're really pleased to see that we remember most of the stuff we learned, because it's thinking skills more than specific solutions.
If you give it a try, feel free to tell us how you like it. :)
Update: Yay! We finished the original 50 levels. That was quite neat. Some really interesting concepts in the later ones around how boxes flow and how you block off your own path as you pack them.
We're pretty sure we'd never gotten all the way through before. Back in the 90s we had a version of this on our calculator, but we lost our progress every time we crashed the calculator...
(Yes, we were the type of people who could get a calculator to crash. Even back then.)
One more thought about state space: Part of how you build that map in your head is by finding ways to carve the possible states into pieces.
One way to do that is to think about the large-scale properties of the puzzle. What are the things that will always be true? What are the things that may change, but not very often?
Are there any aspects of the puzzle that function as "resources" that can be consumed but not replenished?
Invariants like that are, in a sense, just one more type of little lemma you can prove about how the puzzle works. They're a particularly important part though, because they let you start to carve up states that you haven't visited yet.
Like if you know, oh, there's a block at this spot at the beginning but there's no way to ever get another block there... then that block is a non-renewable resource. So you know you should pay careful attention to when you're using it.
Anyway! Puzzles like this aren't something you can teach in a school, because you can't really do this stuff as work. You have to do it for fun, if you're going to get the full experience.
We do believe that it's worthwhile. Have fun. :)
[Special thanks to those of you who helped us figure out Cohost image embeds! This is what we needed them for.]